http://users.ics.aalto.fi/jhollmen/dippa/node22.html
http://www.accaglobal.com/us/en/student/exam-support-resources/fundamentals-exams-study-resources/f5/technical-articles/the-learning-rate-and-learning-effect.html
http://blogs.quovantis.com/k-means-clustering-algorithm-through-apache-spark/
https://github.com/PredictionIO/Programmers-Guide-to-Machine-Intelligence-with-PredictionIO/blob/master/chapter3.md
For matrix factorization we don't tell the algorithm a preset list of features (female vocal, country, PBR&B, etc.). Instead we give the algorithm a chart (matrix)
and ask the algorithm to extract a set of features from this data. To anthropomorphize this yet even more, it is like asking the algorithm, Okay algorithm, given 2 features (or some number of features) call them feature 1 and feature 2, can you come up with the P and Q matrices? These extracted features are not going to be something like 'female vocals' or 'country influence'. In fact, we don't care what these features represent.
We are given matrix R and we would like to estimate P and Q.
http://redmonk.com/fryan/2016/06/06/a-look-at-popular-machine-learning-frameworks/
Salesforce (who recently acquired prediction.io)
http://spark.apache.org/docs/latest/ml-guide.html
http://www.actionml.com/blog/personalized_search
Amazon, another trailblazer in Machine Learning, gave the technique the name "Behavior-Based Search". They describe it as "People who searched for X bought item Y.”
https://github.com/actionml/template-personalized-search
 其中R(m×n)代表用户对商品的评分矩阵,X(m×k)代表用户对隐含特征的偏好矩阵,Y(n×k)表示商品所包含隐含特征的矩阵,T表示矩阵Y的转置。实际中,一般取k<<min(m, n), 也就是相当于降维了。这里的低维矩阵,有的地方也叫低秩矩阵。
其中R(m×n)代表用户对商品的评分矩阵,X(m×k)代表用户对隐含特征的偏好矩阵,Y(n×k)表示商品所包含隐含特征的矩阵,T表示矩阵Y的转置。实际中,一般取k<<min(m, n), 也就是相当于降维了。这里的低维矩阵,有的地方也叫低秩矩阵。

https://en.wikipedia.org/wiki/Least_squares
books
https://www.analyticsvidhya.com/blog/2015/10/read-books-for-beginners-machine-learning-artificial-intelligence/
http://machinelearningmastery.com/6-practical-books-for-beginning-machine-learning/
http://machinelearningmastery.com/best-machine-learning-resources-for-getting-started/
http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html
http://sbp810050504.blog.51cto.com/2799422/1269572
在数学中,一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)
函数关于变量的偏导数写为或。偏导数符号是全导数符号的变体
http://baike.baidu.com/view/1029405.htm
http://baike.baidu.com/view/760381.htm
显微分
先若要找出直线的斜率,只要选取两个点,把坐标代入(y2 - y1)/(x2 - x1)。但是这只适用于直线方程。要是要找曲线的斜率,要找两个点,代入 [f(x + dx) - f(x)]/dx。 Dx表示"delta x," 表示两个x坐标的差。注意这个公式和(y2 - y1)/(x2 - x1)差不多,只不过形式不同。因为曲线上用这种方法会出现偏差,所以要用非直接的方法找出斜率。要找出 (x, f(x))的斜率, dx 要趋于0,于是这两个点会无限接近另一个点。但是分母也不能等于0,所以把两个点的值代入以后,要用因式分解等等方法把分母的dx消掉。消掉后,让dx 等于 0,得出等式。 这就是 (x, f(x))的斜率了。导数是用来找出任何曲线的斜率的一般公式
把等式代入[f(x + dx) - f(x)]/dx。如 y = x2,代入后[(x + dx)2 - x2]/dx.
若写不出y只在一边的的表达式,就要用隐微分来求导了。即便硬要把y写到一边,用 dy/dx 求导也很麻烦。
http://www.accaglobal.com/us/en/student/exam-support-resources/fundamentals-exams-study-resources/f5/technical-articles/the-learning-rate-and-learning-effect.html
http://blogs.quovantis.com/k-means-clustering-algorithm-through-apache-spark/
The first step would be to randomly initialize cluster centroids. In this example I am taking the number of centroids as 2. But this number can vary as to how many unlabelled groups you want to divide your data into.
The second step is Cluster Assignment step. So, we go through each and every data point and depending upon whether it’s closer to Red or Blue Cluster Centroid, color the data points as Red or Blue.
The third step is the Move Centroid step. This step involved moving the each Cluster Centroid to position derived by calculating the mean of the corresponding colored data points. This means Blue point would be moved to the Mean we get from all the Blue data points and similarly for Red.
Step Second and third would be repeated till the time the Cluster Centroid do not move any further.
In this case, the Cost function is the total sum of the squared distance of every point to its corresponding cluster centroid.
The objective of K-Means id to minimize the Cost Function.
int numberOfClusters = 4; int numberOfIterations = 20; KMeansModel clusters = KMeans.train(parsedData.rdd(), numberOfClusters, numberOfIterations); double WSSSE = clusters.computeCost(parsedData.rdd()); System.out.println("Within Set Sum of Squared Errors = " + WSSSE); for (Vector center : clusters.clusterCenters()) { System.out.println(" " + center); }
https://github.com/PredictionIO/Programmers-Guide-to-Machine-Intelligence-with-PredictionIO/blob/master/chapter3.md
For matrix factorization we don't tell the algorithm a preset list of features (female vocal, country, PBR&B, etc.). Instead we give the algorithm a chart (matrix)
and ask the algorithm to extract a set of features from this data. To anthropomorphize this yet even more, it is like asking the algorithm, Okay algorithm, given 2 features (or some number of features) call them feature 1 and feature 2, can you come up with the P and Q matrices? These extracted features are not going to be something like 'female vocals' or 'country influence'. In fact, we don't care what these features represent.
latent features.
The inputs to the matrix factorization algorithm are the data in the chart shown above and the number of latent features to use (for example, 2). Our eventual goal is to calculate $\hat{R}$ a table of estimated ratings. That is, a table similar to the above but with all the numbers filled in
To get these predicted values we use latent features as an intermediary. Let's say we have two features: feature 1 and feature 2. And, to keep things simple, let's just look at how to get Jake's rating of Taylor Swift. Jake's rating is based solely on these two features and for Jake, these features are not equal in importance but are weighed differently. For example, Jake might weigh these features:
| - | Feature 1 | Feature 2 |
|---|---|---|
| Jake | 0.717 | 2.309 |
So feature 2 is much more influential in Jake's rating than feature 1 is.
We are going to have these feature weights for all our users and, again, by convention we call the resulting matrix, P:
The other thing we need is how these features are represented in Taylor Swift-- how much "Feature 1-iness IS Taylor Swift? So we need a table of weights for the artists and again by convention, we call this matrix Q:
This operation is called the dot product. A list of numbers, for example, Jake's weights for the features: [0.717, 2.309] is called a vector. A dot product is performed on two vectors of equal length and produces a single value. It is defined as follows:
This flipping of the table (or matrix) is called transposing the matrix. If the original matrix is called Q the transpose of the matrix is indicated by $Q^T.$ So now when you see $Q^T$ you don't need to freak out. Just think, oh, I just flip the matrix so rows become columns. Cool.
How do we get Matrices P and Q?
There are several common ways to derive these matrices. One method is called stochastic gradient descent. The basic idea is this. We are going to randomly select values for P and Q. For example, we would randomly select initial values for Jake:
Jake = [0.03, 0.88]
and randomly select initial values for Taylor Swift:
Taylor = [ 0.73, 0.49]
So with those initial ratings we get a prediction of $$J \cdot S = 0.03 \times 0.73 + 0.88 \times 0.49 = 0.45$$
which is a particularly bad guess considering Jake really gave Taylor Swift a '5'. So we adjust those values. We underestimated Jake's rating of Taylor Swift so we boost maybe something like:
Jake = [0.12, 0.83]
Taylor = [ 0.80, 0.47]
and now we get:
$$J \cdot S = 0.12 \times 0.80 + 0.83 \times 0.47 = 0.49$$
That is better than before but still we underestimated so we adust and try again. And adjust and try again. We repeat this process thousands of times until our predicted values get close to the actual values. The general algorithm is
- generate random values for the P and Q matrices
- using these P and Q matrices estimate the ratings (for ex., Jake's rating of Taylor Swift).
- compute the error between the actual rating and our estimated rating (for example, Jake actually gave Taylor Swift a '5' but using P and Q we estimated the rating to be 0.45. Our error was 4.55.
- using this error adjust P and Q to improve our estimate
- If our total error rate is small enough or we have gone through a bunch of iterations (for ex., 4000) terminate the algorithm. Else go to step 2.
For how simple this algorithm is, it works surprisingly well.
The other method of estimated P and Q is called alternating least squares or ALS and this is the one our PredictionIO recommendation engine uses.
ALSWe are given matrix R and we would like to estimate P and Q.
we could determine how much each customer liked country and PBR&B. We also saw that if we had the matrix of users rating different artists and a matrix representing how much each customer liked country and PBR&B, then we could determine the country and PBR&B influences for each artist. So as long as we had two of the matrices we could determine the third. Unfortunately we only have one of the matrices, not two. It seems we are stuck. But there is a way to bootstrap our way of of this problem. We simply randomly guess the values of one of the other two matrices. Suppose we guess at the values of Q. Now we have two matrices, R and Q and we can determine P. Now we have all three matrices but for Q we just took a random guess, so it is a bit dodgy. But that is okay because now we have P, and with P and R we can determine a better guess for Q. So we do that.
Now P is a bit dodgy as well since it was based on our original wild guess for Q, but now that we have a better value for Q we can use that to recompute P. So the algorithm is this.
- compute random values for Q
- use that and R to compute P
- use that and R to compute Q
- while we haven't reached the max number of iterations go to 2.
The word alternating in alternating least squares is based on us alternating our computations of P and Q. Now you may be wondering what the least squares bit means. We are given the matrix R and initially we compute random values for Q. Then, using R and Q we are going to compute the best possible P. But what do we mean by best possible? Let's say R the ratings customers gave artists is:
| Customer | Taylor Swift | Miranda Lambert | Jhené Aiko | The Weeknd |
|---|---|---|---|---|
| Jake | 5 | ? | 2 | 2 |
| Ann | 2 | ? | 5 | ? |
and using the Q and R matrices we get $\hat{R}$ our estimate of R.
| Customer | Taylor Swift | Miranda Lambert | Jhené Aiko | The Weeknd |
|---|---|---|---|---|
| Jake | 2.5 | ? | 1.0 | 3.5 |
| Ann | 5.0 | ? | 3.5 | ? |
So how good of a guess is it? Well, let's see. Jake really gave Taylor Swift a 5 and our algorithm predicted a 2.5. That is 2.5 different. And Jake gave Jhené Aiko a 2 and our algorithm predicted a 1. That is 1 different. It sounds like a good idea might be to add up all these differences. The one twist we do is square the difference. So for each artist we subtract what our algorithm predicted from Jake's actual rating and square that. Then we sum those up:
$$SquaredError = (5-2.5)^2 + (2 - 1)^2 + (2 - 3.5)^2 + (2 - 5)^2 + (5 - 3.5)^2$$$ = 6.25 + 1 + 2.25 + 9 + 2.25 = 20.75
The smaller this number is, the closer our estimate is to Jake's real ratings. So to start we have the real ratings $R$ and our guess for Q and using those we are going to select a P which has results in the smallest squared error. Once we have this P we hold it constant and use it and $R$ to determine the Q that results in the least squared error and so on. So the least squares bit of Alternating Least Squares means using this measure to compute how close our estimate is to the real ratings.
https://github.com/actionml/template-personalized-searchhttp://redmonk.com/fryan/2016/06/06/a-look-at-popular-machine-learning-frameworks/
Salesforce (who recently acquired prediction.io)
http://spark.apache.org/docs/latest/ml-guide.html
The MLlib RDD-based API is now in maintenance mode.
As of Spark 2.0, the RDD-based APIs in the
spark.mllib package have entered maintenance mode. The primary Machine Learning API for Spark is now the DataFrame-based API in the spark.ml package.
MLlib uses the linear algebra package Breeze, which depends on netlib-java for optimised numerical processing. If native libraries1 are not available at runtime, you will see a warning message and a pure JVM implementation will be used instead.
Due to licensing issues with runtime proprietary binaries, we do not include
netlib-java’s native proxies by default. To configure netlib-java / Breeze to use system optimised binaries, include com.github.fommil.netlib:all:1.1.2 (or build Spark with -Pnetlib-lgpl) as a dependency of your project and read the netlib-java documentation for your platform’s additional installation instructions.
Association rule learning is a rule-based machine learning method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using some measures of interestingness
关联规则学习(英语:Association rule learning)是一种在大型数据库中发现变量之间的有趣性关系的方法。它的目的是利用一些有趣性的量度来识别数据库中发现的强规则
基于强规则的概念,Rakesh Agrawal等人[2]引入了关联规则以发现由超市的POS系统记录的大批交易数据中产品之间的规律性。例如,从销售数据中发现的规则 {洋葱, 土豆}→{汉堡} 会表明如果顾客一起买洋葱和土豆,他们也有可能买汉堡的肉。此类信息可以作为做出促销定价或产品植入等营销活动决定的根据。除了上面购物篮分析中的例子以外, 关联规则如今还被用在许多应用领域中,包括网络用法挖掘、入侵检测、连续生产及生物信息学中。与序列挖掘相比,关联规则学习通常不考虑在、事务中或事务间的项目的顺序。
the problem of association rule mining is defined as:
Let be a set of binary attributes called items.
Let be a set of transactions called the database.
Each transaction in has a unique transaction ID and contains a subset of the items in .
A rule is defined as an implication of the form:
Where and .
Every rule is composed by two different sets of items, also known as itemsets, and , where is called antecedent or left-hand-side (LHS) and consequent or right-hand-side (RHS).
To illustrate the concepts, we use a small example from the supermarket domain. The set of items is and in the table is shown a small database containing the items, where, in each entry, the value 1 means the presence of the item in the corresponding transaction, and the value 0 represents the absence of an item in that transaction.
An example rule for the supermarket could be meaning that if butter and bread are bought, customers also buy milk.
Support is an indication of how frequently the item-set appears in the database.
The support value of with respect to is defined as the proportion of transactions in the database which contains the item-set . In formula:
In the example database, the item-set has a support of since it occurs in 20% of all transactions (1 out of 5 transactions). The argument of is a set of preconditions, and thus becomes more restrictive as it grows (instead of more inclusive)
Confidence is an indication of how often the rule has been found to be true.
The confidence value of a rule, , with respect to a set of transactions , is the proportion of the transactions that contains which also contains .
Confidence is defined as:
.
For example, the rule has a confidence of in the database, which means that for 100% of the transactions containing butter and bread the rule is correct (100% of the times a customer buys butter and bread, milk is bought as well).
http://www.actionml.com/blog/personalized_search
Amazon, another trailblazer in Machine Learning, gave the technique the name "Behavior-Based Search". They describe it as "People who searched for X bought item Y.”
https://github.com/actionml/template-personalized-search
ALS
ALS是alternating least squares的缩写 , 意为交替最小二乘法;而ALS-WR是alternating-least-squares with weighted-λ -regularization的缩写,意为加权正则化交替最小二乘法。该方法常用于基于矩阵分解的推荐系统中。例如:将用户(user)对商品(item)的评分矩阵分解为两个矩阵:一个是用户对商品隐含特征的偏好矩阵,另一个是商品所包含的隐含特征的矩阵。在这个矩阵分解的过程中,评分缺失项得到了填充,也就是说我们可以基于这个填充的评分来给用户最商品推荐了。
由于评分数据中有大量的缺失项,传统的矩阵分解SVD(奇异值分解)不方便处理这个问题,而ALS能够很好的解决这个问题。对于R(m×n)的矩阵,ALS旨在找到两个低维矩阵X(m×k)和矩阵Y(n×k),来近似逼近R(m×n),即:
为了找到使低秩矩阵X和Y尽可能地逼近R,需要最小化下面的平方误差损失函数:
损失函数一般需要加入正则化项来避免过拟合等问题,我们使用L2正则化,所以上面的公式改造为:
到这里,协同过滤就成功转化成了一个优化问题。由于变量xu和yi耦合到一起,这个问题并不好求解,所以我们引入了ALS,也就是说我们可以先固定Y(例如随机初始化X),然后利用公式(2)先求解X,然后固定X,再求解Y,如此交替往复直至收敛,即所谓的交替最小二乘法求解法。
具体求解方法说明如下:
- 先固定Y, 将损失函数L(X,Y)对xu求偏导,并令导数=0,得到:
- 同理固定X,可得:
- 迭代步骤:首先随机初始化Y,利用公式(3)更新得到X, 然后利用公式(4)更新Y, 直到均方根误差变RMSE化很小或者到达最大迭代次数。
ALS-WR
上文提到的模型适用于解决有明确评分矩阵的应用场景,然而很多情况下,用户没有明确反馈对商品的偏好,也就是没有直接打分,我们只能通过用户的某些行为来推断他对商品的偏好。比如,在电视节目推荐的问题中,对电视节目收看的次数或者时长,这时我们可以推测次数越多,看得时间越长,用户的偏好程度越高,但是对于没有收看的节目,可能是由于用户不知道有该节目,或者没有途径获取该节目,我们不能确定的推测用户不喜欢该节目。ALS-WR通过置信度权重来解决这些问题:对于更确信用户偏好的项赋以较大的权重,对于没有反馈的项,赋以较小的权重。ALS-WR模型的形式化说明如下:
Collaborative Filtering (CF) is a method of making automatic predictions about the interests of a user by learning its preferences (or taste) based on information of his engagements with a set of available items, along with other users’ engagements with the same set of items. in other words, CF assumes that, if a person A has the same opinion as person B on some set of issues X={x1,x2,…}, then A is more likely to have B‘s opinion on a new issue y than to have the opinion of any other person that doesn’t agree with A on X.
One of the most popular algorithms to solve co-clustering problems (and specifically for collaborative recommender systems) is called Matrix Factorization (MF). In its simplest form, it assumes a matrix 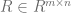 of ratings given by musers to nitems. Applying this technique on R will end up factorizing R into two matrices
of ratings given by musers to nitems. Applying this technique on R will end up factorizing R into two matrices 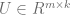 and
and 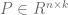 such that
such that 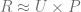 (their multiplication approximates R).
(their multiplication approximates R).

Note that this algorithm introduces a new quantity, k, that serves as both U‘s and P‘s dimensions. This is the rank of the factorization. Formally, each 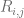 is factorized into the dot product of
is factorized into the dot product of 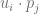 , having
, having 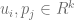 . Intuitively, this model assumes every rating in R is affected by k effects. Moreover, it represents both users and items in U and Paccordingly, in terms of those k effects.
. Intuitively, this model assumes every rating in R is affected by k effects. Moreover, it represents both users and items in U and Paccordingly, in terms of those k effects.
The problem is, how to form those categories efficiently. Hell, it can even depends of certain affinity to some movie actors, directors, language, location of filming, and more, and the number of possible features to create is immense.
Regression estimates are used to describe data and to explain the relationship between one dependent variable and one or more independent variables.
At the center of the regression analysis is the task of fitting a single line through a scatter plot. The simplest form with one dependent and one independent variable is defined by the formula y = c + b*x, where y = estimated dependent, c = constant, b = regression coefficients, and x = independent variable.
It consists of 3 stages – (1) analyzing the correlation and directionality of the data, (2) estimating the model, i.e., fitting the line, and (3) evaluating the validity and usefulness of the model.
Linear regression consists of finding the best-fitting straight line through the points. The best-fitting line is called a regression line.
The error of prediction for a point is the value of the point minus the predicted value (the value on the line).
the best-fitting line is the line that minimizes the sum of the squared errors of prediction
MX is the mean of X, MY is the mean of Y, sX is the standard deviation of X, sY is thestandard deviation of Y, and r is the correlation between X and Y.
| MX | MY | sX | sY | r |
|---|---|---|---|---|
| 3 | 2.06 | 1.581 | 1.072 | 0.627 |
The slope (b) can be calculated as follows:
b = r sY/sX
and the intercept (A) can be calculated as
A = MY - bMX.
https://en.wikipedia.org/wiki/Least_squares
The method of least squares is a standard approach in regression analysis to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in the results of every single equation.
The most important application is in data fitting. The best fit in the least-squares sense minimizes the sum of squared residuals, a residual being the difference between an observed value and the fitted value provided by a model.
Ordinary Least Squares (OLS)
Ordinary Least Squares or OLS is one of the simplest (if you can call it so) methods of linear regression. The goal of OLS is to closely "fit" a function with the data. It does so by minimizing the sum of squared errors from the data.
These two models each have an intercept term , and a slope term (some textbooks use instead of and instead of , this is a much better approach once we move to multivariate formulas). We can represent an arbitrary single variable model with the formula: The y-values are related to the x-values given this formula. We use the subscript i to denote an observation. So is paired with , with , etc. The term is the error term, which is the difference between the effect of and the observed value of .
Unfortunately, we don't know the values of or . We have to approximate them. We can do this by using the ordinary least squares method. The term "least squares" means that we are trying to minimize the sum of squares, or more specifically we are trying to minimize the squared error terms. Since there are two variables that we need to minimize with respect to ( and ), we have two equations:
Call the solutions to these equations and . Solving we get:
Where and . Computing these results can be left as an exercise.
Call the solutions to these equations and . Solving we get:
Where and . Computing these results can be left as an exercise.
It is important to know that and are not the same as and because they are based on a single sample rather than the entire population. If you took a different sample, you would get different values for and . Let's call and the OLS estimators of and . One of the main goals of econometrics is to analyze the quality of these estimators and see under what conditions these are good estimators and under which conditions they are not.
Once we have and , we can construct two more variables. The first is the fitted values, or estimates of y:
The second is the estimates of the error terms, which we will call the residuals:
The second is the estimates of the error terms, which we will call the residuals:
Statistical regression is basically a way to predict unknown quantities from a batch of existing data.
OLS is concerned with the squares of the errors. It tries to find the line going through the sample data that minimizes the sum of the squared errors. Below, the squared errors are represented as squares, and your job is to choose betas (the slope and intercept of the regression line) so that the total
OLS works exactly the same with more. Below is OLS with two independent variables. Instead of the errors being relative to a line, though, they're now relative to a plane in 3D space.
books
https://www.analyticsvidhya.com/blog/2015/10/read-books-for-beginners-machine-learning-artificial-intelligence/
http://machinelearningmastery.com/6-practical-books-for-beginning-machine-learning/
http://machinelearningmastery.com/best-machine-learning-resources-for-getting-started/
http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html
监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
http://sbp810050504.blog.51cto.com/2799422/1269572
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
某次实验得到了四个数据点 :、、、(右图中红色的点)。我们希望找出一条和这四个点最匹配的直线 ,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的 和 :
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
最小值可以通过对 分别求 和 的偏导数,然后使它们等于零得到。
如此就得到了一个只有两个未知数的方程组,很容易就可以解出:
也就是说直线 是最佳的。
导数(英语:Derivative)是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数的自变量在一点上产生一个增量时,函数输出值的增量与自变量增量的比值在趋于0时的极限如果存在,即为在处的导数,记作、或。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度[1]:153。
导数是函数的局部性质。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。如果函数的自变量和取值都是实数的话,那么函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
对于可导的函数,也是一个函数,称作的导函数。寻找已知的函数在某点的导数或其导函数的过程称为求导。反之,已知导函数也可以倒过来求原来的函数
设有定义域和取值都在实数域中的函数 。若 在点 的某个邻域内有定义,则当自变量 在 处取得增量 (点 仍在该邻域内)时,相应地幔数 取得增量 ;如果 与 之比当 时的极限存在,则称函数 在点 处可导,并称这个极限为函数 在点 处的导数,记为 ,即:[2]:117-118
也可记作 、 、 或 [1]:154。
对于一般的函数,如果不使用增量的概念,函数 在点 处的导数也可以定义为:当定义域内的变量 趋近于 时,
函数y=f(x)在x0点的导数f'(x0)的几何意义:表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。
在数学中,一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)
函数关于变量的偏导数写为或。偏导数符号是全导数符号的变体
也就是说,每一个x的值定义了一个函数,记为fx,它是一个一元函数。也就是说:
- 。
一旦选择了一个x的值,例如a,那么f(x,y)便定义了一个函数fa,把y映射到a2 + ay + y2:
- 。
在这个表达式中,a是常数,而不是变量,因此fa是只有一个变量的函数,这个变量是y。这样,便可以使用一元函数的导数的定义:
- 。
以上的步骤适用于任何a的选择。把这些导数合并起来,便得到了一个函数,它描述了f在y方向上的变化:
- 。
偏导数f'x(x0,y0)表示固定面上一点对x轴的切线斜率;偏导数f'y(x0,y0)表示固定面上一点对y轴的切线斜率。
高阶偏导数:如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy.
http://baike.baidu.com/view/760381.htm
⑴求函数y=f(x)在x0处导数的步骤:
① 求函数的增量Δy=f(x0+Δx)-f(x0)
② 求平均变化率
③ 取极限,得导数。
⑵基本初等函数的导数公式:
1 .C'=0(C为常数);
2 .(Xn)'=nX(n-1) (n∈Q);
3 .(sinX)'=cosX;
4 .(cosX)'=-sinX;
5 .(aX)'=aXIna (ln为自然对数)
特别地,(ex)'=ex
6 .(logaX)'=(1/X)logae=1/(Xlna) (a>0,且a≠1)
特别地,(ln x)'=1/x
7 .(tanX)'=1/(cosX)2=(secX)2
8 .(cotX)'=-1/(sinX)2=-(cscX)2
9 .(secX)'=tanX secX
10.(cscX)'=-cotX cscX
⑶导数的四则运算法则:
①(u±v)'=u'±v'
②(uv)'=u'v+uv'
③(u/v)'=(u'v-uv')/ v2
http://zh.wikihow.com/%E5%9C%A8%E5%BE%AE%E7%A7%AF%E5%88%86%E4%B8%AD%E6%B1%82%E5%AF%BC显微分
先若要找出直线的斜率,只要选取两个点,把坐标代入(y2 - y1)/(x2 - x1)。但是这只适用于直线方程。要是要找曲线的斜率,要找两个点,代入 [f(x + dx) - f(x)]/dx。 Dx表示"delta x," 表示两个x坐标的差。注意这个公式和(y2 - y1)/(x2 - x1)差不多,只不过形式不同。因为曲线上用这种方法会出现偏差,所以要用非直接的方法找出斜率。要找出 (x, f(x))的斜率, dx 要趋于0,于是这两个点会无限接近另一个点。但是分母也不能等于0,所以把两个点的值代入以后,要用因式分解等等方法把分母的dx消掉。消掉后,让dx 等于 0,得出等式。 这就是 (x, f(x))的斜率了。导数是用来找出任何曲线的斜率的一般公式
把等式代入[f(x + dx) - f(x)]/dx。如 y = x2,代入后[(x + dx)2 - x2]/dx.
把因子展开成[dx(2x + dx)]/dx。 把上下两个dx消去。得到2x + dx,让dx 趋近 0, 得到2x。这表示任何y = x2 曲线的斜率是 2x。代入x,得到一个点的斜率
- 任何次数的导数都是次数乘以原方程-1次。比如x5 的导数是 5x4, x3.5 导数是 3.5x2.5。若x前已有数字,直接和次数相乘就行。如3x4 求导得12x3。
- 任何常数的导数是0。 8 的导数是0
- 和的导数是导数的和。比如 x3 + 3x2 求导得3x2 + 6x
- 积的导数是第一项乘以后一项的导数加上后一项乘以前一项的导数。如 x3(2x + 1) 得 x3(2) + (2x + 1)3x2,即8x3 + 3x2
- 商的导数是(假设是 f/g形式) [g(f导数) - f(g导数)]/g2。(x2 + 2x - 21)/(x - 3) 求导得 (x2- 6x + 15)/(x - 3)2。
若写不出y只在一边的的表达式,就要用隐微分来求导了。即便硬要把y写到一边,用 dy/dx 求导也很麻烦。
 be a set of
be a set of  binary attributes called items.
binary attributes called items. be a set of transactions called the database.
be a set of transactions called the database. has a unique transaction ID and contains a subset of the items in
has a unique transaction ID and contains a subset of the items in  .
.
 and
and  .
. and
and  , where
, where  and in the table is shown a small database containing the items, where, in each entry, the value 1 means the presence of the item in the corresponding transaction, and the value 0 represents the absence of an item in that transaction.
and in the table is shown a small database containing the items, where, in each entry, the value 1 means the presence of the item in the corresponding transaction, and the value 0 represents the absence of an item in that transaction. meaning that if butter and bread are bought, customers also buy milk.
meaning that if butter and bread are bought, customers also buy milk. is defined as the proportion of transactions in the database which contains the item-set
is defined as the proportion of transactions in the database which contains the item-set 
 has a support of
has a support of  since it occurs in 20% of all transactions (1 out of 5 transactions). The argument of
since it occurs in 20% of all transactions (1 out of 5 transactions). The argument of  is a set of preconditions, and thus becomes more restrictive as it grows (instead of more inclusive)
is a set of preconditions, and thus becomes more restrictive as it grows (instead of more inclusive) .
. in the database, which means that for 100% of the transactions containing butter and bread the rule is correct (100% of the times a customer buys butter and bread, milk is bought as well).
in the database, which means that for 100% of the transactions containing butter and bread the rule is correct (100% of the times a customer buys butter and bread, milk is bought as well).


 , and a slope term
, and a slope term  (some textbooks use
(some textbooks use  instead of
instead of  instead of
instead of  The y-values are related to the x-values given this formula. We use the subscript i to denote an observation. So
The y-values are related to the x-values given this formula. We use the subscript i to denote an observation. So  is paired with
is paired with  ,
,  with
with  , etc. The
, etc. The  term is the error term, which is the difference between the effect of
term is the error term, which is the difference between the effect of  and the observed value of
and the observed value of  .
. or
or 


 and
and  . Solving we get:
. Solving we get:

 and
and  . Computing these results can be left as an exercise.
. Computing these results can be left as an exercise.

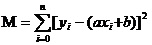
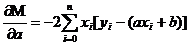
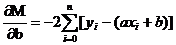
 :
: 、
、 、
、 、
、 (右图中红色的点)。我们希望找出一条和这四个点最匹配的直线
(右图中红色的点)。我们希望找出一条和这四个点最匹配的直线  ,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的
,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的  :
:
![{\begin{aligned}S(\beta _{1},\beta _{2})=&\left[6-(\beta _{1}+1\beta _{2})\right]^{2}+\left[5-(\beta _{1}+2\beta _{2})\right]^{2}\\&+\left[7-(\beta _{1}+3\beta _{2})\right]^{2}+\left[10-(\beta _{1}+4\beta _{2})\right]^{2}.\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a54ff2e6eab2c0875cc498b93854f1ad7493ae6)
 分别求
分别求 



 是最佳的。
是最佳的。 的自变量在一点
的自变量在一点 上产生一个增量
上产生一个增量 时,函数输出值的增量与自变量增量
时,函数输出值的增量与自变量增量 、
、 或
或 。例如在
。例如在 也是一个函数,称作
也是一个函数,称作 。若
。若  在点
在点  的某个
的某个 在
在  (点
(点  仍在该邻域内)时,相应地幔数
仍在该邻域内)时,相应地幔数  取得增量
取得增量  ;如果
;如果  与
与  之比当
之比当  时的极限存在,则称函数
时的极限存在,则称函数  在点
在点  ,即:
,即:
 、
、  、
、  处的导数也可以定义为:当定义域内的变量
处的导数也可以定义为:当定义域内的变量  趋近于
趋近于 





 。
。 。
。 。
。 。
。