SSTable + LSM tree - Cassandra + LevelDB

https://github.com/facebook/rocksdb/wiki/MemTable

MemTable is an in-memory data-structure holding data before they are flushed to SST files. It serves both read and write - new writes always insert data to memtable, and reads has to query memtable before reading from SST files, because data in memtable is newer. Once a memtable is full, it becomes immutable and replace by a new memtable. A background thread will flush the content of the memtable into a SST file, after which the memtable can be destroyed.

The default implementation of memtable is based on skiplist. Other than the default memtable implementation, users can use other types of memtable implementation, for example HashLinkList, HashSkipList or Vector, to speed-up some queries.

Skiplist MemTable

Skiplist-based memtable provides general good performance to both read and write, random access and sequential scan. Besides, it provides some other useful features that other memtable implementations don't currently support, like Concurrent Insert and Insert with Hint.

HashSkiplist MemTable

As their names imply, HashSkipList organizes data in a hash table with each hash bucket to be a skip list, while HashLinkList organizes data in a hash table with each hash bucket as a sorted single linked list. Both types are built to reduce number of comparisons when doing queries. One good use case is to combine them with PlainTable SST format and store data in RAMFS.

When doing a look-up or inserting a key, target key's prefix is retrieved using Options.prefix_extractor, which is used to find the hash bucket. Inside a hash bucket, all the comparisons are done using whole (internal) keys, just as SkipList based memtable.

The biggest limitation of the hash based memtables is that doing scan across multiple prefixes requires copy and sort, which is very slow and memory costly.

Skiplist MemTable

Skiplist-based memtable provides general good performance to both read and write, random access and sequential scan. Besides, it provides some other useful features that other memtable implementations don't currently support, like Concurrent Insert and Insert with Hint.

HashSkiplist MemTable

As their names imply, HashSkipList organizes data in a hash table with each hash bucket to be a skip list, while HashLinkList organizes data in a hash table with each hash bucket as a sorted single linked list. Both types are built to reduce number of comparisons when doing queries. One good use case is to combine them with PlainTable SST format and store data in RAMFS.

When doing a look-up or inserting a key, target key's prefix is retrieved using Options.prefix_extractor, which is used to find the hash bucket. Inside a hash bucket, all the comparisons are done using whole (internal) keys, just as SkipList based memtable.

The biggest limitation of the hash based memtables is that doing scan across multiple prefixes requires copy and sort, which is very slow and memory costly.

Flush

There are three scenarios where memtable flush can be triggered:

1. Memtable size exceed write_buffer_size after a write.
2. Total memtable size across all column families exceed db_write_buffer_size, or write_buffer_manager signals a flush. In this scenario the largest memtable will be flushed.
3. Total WAL file size exceed max_total_wal_size. In this scenario the memtable with the oldest data will be flushed, in order to allow the WAL file with data from this memtable to be purged.

As a result, a memtable can be flushed before it is full. This is one reason the generated SST file can be smaller than the corresponding memtable. Compression is another factor to make SST file smaller than corresponding memtable, since data in memtable is uncompressed.

Concurrent Insert

Without support of concurrent insert to memtables, concurrent writes to RocksDB from multiple threads will apply to memtable sequentially. Concurrent memtable insert is enabled by default and can be turn off via allow_concurrent_memtable_write option, although only skiplist-based memtable supports the feature.

Insert with Hint

In-place Update

Comparison

Mem Table Type	SkipList	HashSkipList	HashLinkList	Vector
Optimized Use Case	General	Range query within a specific key prefix	Range query within a specific key prefix and there are only a small number of rows for each prefix	Random write heavy workload
Index type	binary search	hash + binary search	hash + linear search	linear search
Support totally ordered full db scan?	naturally	very costly (copy and sort to create a temporary totally-ordered view)	very costly (copy and sort to create a temporary totally-ordered view)	very costly (copy and sort to create a emporary totally-ordered view)
Memory Overhead	Average (multiple pointers per entry)	High (Hash Buckets + Skip List Metadata for non-empty buckets + multiple pointers per entry)	Lower (Hash buckets + pointer per entry)	Low (pre-allocated space at the end of vector)
MemTable Flush	Fast with constant extra memory	Slow with high temporary memory usage	Slow with high temporary memory usage	Slow with constant extra memory
Concurrent Insert	Support	Not support	Not support	Not support
Insert with Hint	Support (in case there are no concurrent insert)	Not support	Not support	Not support

https://www.igvita.com/2012/02/06/sstable-and-log-structured-storage-leveldb/
Protocol Buffers is the lingua franca of individual data record at Google.
SSTable is a simple abstraction to efficiently store large numbers of key-value pairs while optimizing for high throughput, sequential read/write workloads.

SSTable: Sorted String Table

A "Sorted String Table" then is exactly what it sounds like, it is a file which contains a set of arbitrary, sorted key-value pairs inside. Duplicate keys are fine, there is no need for "padding" for keys or values, and keys and values are arbitrary blobs. Read in the entire file sequentially and you have a sorted index. Optionally, if the file is very large, we can also prepend, or create a standalone key:offset index for fast access. That's all an SSTable is: very simple, but also a very useful way to exchange large, sorted data segments.

SSTable and BigTable: Fast random access?

Once an SSTable is on disk it is effectively immutable because an insert or delete would require a large I/O rewrite of the file. Having said that, for static indexes it is a great solution: read in the index, and you are always one disk seek away, or simply memmap the entire file to memory. Random reads are fast and easy.

Random writes are much harder and expensive, that is, unless the entire table is in memory, in which case we're back to simple pointer manipulation. Turns out, this is the very problem that Google's BigTable set out to solve: fast read/write access for petabyte datasets in size, backed by SSTables underneath. How did they do it?

SSTables and Log Structured Merge Trees

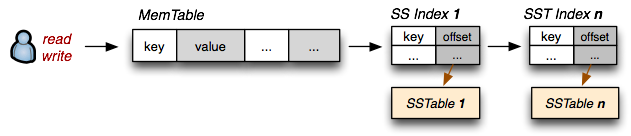
We want to preserve the fast read access which SSTables give us, but we also want to support fast random writes. Turns out, we already have all the necessary pieces: random writes are fast when the SSTable is in memory (let's call itMemTable), and if the table is immutable then an on-disk SSTable is also fast to read from. Now let's introduce the following conventions:

1. On-disk SSTable indexes are always loaded into memory
2. All writes go directly to the MemTable index
3. Reads check the MemTable first and then the SSTable indexes
4. Periodically, the MemTable is flushed to disk as an SSTable
5. Periodically, on-disk SSTables are "collapsed together"

What have we done here? Writes are always done in memory and hence are always fast. Once the MemTable reaches a certain size, it is flushed to disk as an immutable SSTable. However, we will maintain all the SSTable indexes in memory, which means that for any read we can check the MemTable first, and then walk the sequence of SSTable indexes to find our data. Turns out, we have just reinvented the "The Log-Structured Merge-Tree" (LSM Tree), described by Patrick O'Neil, and this is also the very mechanism behind "BigTable Tablets".

LSM & SSTables: Updates, Deletes and Maintenance

This "LSM" architecture provides a number of interesting behaviors: writes are always fast regardless of the size of dataset (append-only), and random reads are either served from memory or require a quick disk seek. However, what about updates and deletes?

Once the SSTable is on disk, it is immutable, hence updates and deletes can't touch the data. Instead, a more recent value is simply stored in MemTable in case of update, and a "tombstone" record is appended for deletes. Because we check the indexes in sequence, future reads will find the updated or the tombstone record without ever reaching the older values! Finally, having hundreds of on-disk SSTables is also not a great idea, hence periodically we will run a process to merge the on-disk SSTables, at which time the update and delete records will overwrite and remove the older data.

SSTables and LevelDB

• SSTable under the hood, MemTable for writes
• Keys and values are arbitrary byte arrays
• Support for Put, Get, Delete operations
• Forward and backward iteration over data
• Built-in Snappy compression

Designed to be the engine for IndexDB in WebKit (aka, embedded in your browser), it is easy to embed, fast, and best of all, takes care of all the SSTable and MemTable flushing, merging and other gnarly details.

 what makes the SSTable fast (sorted and immutable) is also what exposes its very limitations. To address this, we've introduced the idea of a MemTable, and a set of "log structured" processing conventions for managing the many SSTables.

http://codrspace.com/b441berith/cassandra-sstable-memtable-inside/

In-memory SSTable - Memtable.

• Indices from SSTable are loaded to RAM
• Reads - first from Memtable, if data exists but not cached in memory - load from SSTable
• Periodically Memtable is dumped to SSTable
• Periodically on-disk SSTable is merged to 1 file (compaction). Compaction procedure happens when N SStables are being stored, the default N is 4.

All writes are logged to CommitLog to prevent data failure on crashes, when last Memtable changes haven't been swapped. Since SSTable is immutable, updates/deletions are added to Memtable. Deleted records are marked as 'tombstone'. Inserts and deletions are called 'mutations'. Flushes can be triggered using JMX.

LSM trees

LSM tree (The Log-Structured Merge-Tree) - underlying data structure behind SSTable and Memtable. LSM tree contains of small in-memory tree and a large (complete) data tree. Inserts are fast. More details in the original article (1996):http://nosqlsummer.org/paper/lsm-tree

The same concept with SSTable, Memtable and LSM trees is also used in Hbase, LevelDB and, in some way, Google BigTable.

Commit log

Commit log allocates segments (128 mb by default) for data. Once all the changes are written to SSTable, segment is marked as free again. Commits can be batched in settings. 

http://wiki.apache.org/cassandra/ArchitectureCommitLog

Recovery during a restart,

• Each CommitLogSegment is iterated in ascending time order.
• The segment is read from the lowest replay offset among the ReplayPositions read from the SSTable metadata.
• For each log entry read, the log is replayed for a ColumnFamily CF if the position of the log entry is no less than the ReplayPosition for CF in the most recent !SSTable metadata.
• When log replay is done, all Memtables are force flushed to disk and all commitlog segments are recycled.

http://www.slideshare.net/ChrisLohfink1/lsm-trees-37683710
Cassandra Ugly: repairs

●An LSM-tree is composed of two or more tree-like components, each optimized for their type of storage

oA small in-memory tree

oOne or more on disk trees

●Used in Cassandra, HBase, LevelDB, Google Big Table, SQLite4 & more

One tree in memory, one or more on disk
MemTable + SSTable

https://blog.acolyer.org/2014/11/26/the-log-structured-merge-tree-lsm-tree/
The LSM tree is a data structure designed to provide low-cost indexing for files experiencing a high rate of inserts (and deletes) over an extended period.

LSM trees cascade data over time from smaller, higher performing (but more expensive) stores to larger less performant (and less expensive) stores.

The LSM-tree uses an algorithm that defers and batches index changes, cascading the changes from a memory-based component through one or more disk components in an efficient manner reminiscent of merge sort. … it is most useful in applications where index inserts are more common than finds that retrieve the entries. This seems to be a common property for History tables and log files, for example.

The only thing that is required for LSM trees to give an advantage is a high update rate compared to the retrieval rate

ining the index paramount. At the same time find access needs to be frequent enough that an index of some kind must be maintained, because a sequential search through all the records would be out of the question.

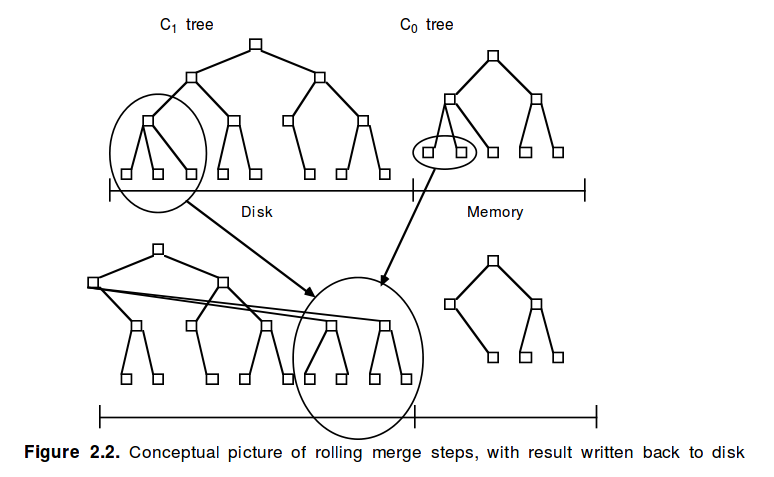
An LSM-tree is composed of two or more tree-like component data structures. For example, a two component LSM-tree has a smaller component which is entirely memory resident, known as the C0 tree (or C0 component), and a larger component which is resident on disk, known as the C1 tree (or C1 component).

Note that although the C1 tree resides on disk, frequently referenced page nodes will still reside in memory in memory buffers. Dath is first inserted into C0, and from there it migrates to C1.

The index entry for [an insert] is inserted into the memory resident C0 tree, after which it will in time migrate out to the C1 tree on disk; any search for an index entry will look first in C0 and then in C1. There is a certain amount of latency (delay) before entries in the C0 tree migrate out to the disk resident C1 tree, implying a need for recovery of index entries that don’t get out to disk prior to a crash.

It’s very cheap to insert an entry into the memory-resident C0 tree, but the cost / capacity of memory compared to disk limits the size of what it makes sense to keep in memory.

At the heart of the LSM algorithm is a rolling merge process:

We need an efficient way to migrate entries out to the C1 tree that resides on the lower cost disk medium. To achieve this, whenever the C0 tree as a result of an insert reaches a threshold size near the maximum allotted, an ongoing rolling merge process serves to delete some contiguous segment of entries from the C0 tree and merge it into the C1 tree on disk.

The rolling merge proceeds one block at at time from the downstream tree (C1 in our example). A block is read in and entries from the upstream tree (C0) are merged with it. This reduces the size of the C0 tree, and creates a new merged C1 block that is written out to disk.

The rolling merge acts in a series of merge steps. A read of a multi-page block containing leaf nodes of the C1 tree makes a range of entries in C1 buffer resident. Each merge step then reads a disk page sized leaf node of the C1 tree buffered in this block, merges entries from the leaf node with entries taken from the leaf level of the C0 tree, thus decreasing the size of C0, and creates a newly merged leaf node of the C1 tree.

Newly merged blocks are written to new disk positions, so that the old blocks will not be over-written and will be available for recovery in case of a crash…. We picture the rolling merge process in a two component LSM-tree as having a conceptual cursor which slowly circulates in quantized steps through equal key values of the C0 tree and C1 tree components, drawing indexing data out from the C0 tree to the C1 tree on disk.

The best efficiency gains over B-tree based systems (the prior art) come when reads and writes are in multi-page blocks thus eliminating seek time.

Finds simply need to work through the trees in order:

When an exact-match find or range find requiring immediate response is performed through the LSM-tree index, first the C0 tree and then the C1 tree is searched for the value or values desired.

We can generalize from a two-component LSM tree to one with k components:

…we define a multi component LSM-tree as having components C0, C1, C2, . . ., CK-1 and CK, indexed tree structures of increasing size, where C0 is memory resident and all other components are disk resident. There are asynchronous rolling merge processes in train between all component pairs (Ci-1, Ci) that move entries out from the smaller to the larger component each time the smaller component, Ci-1, exceeds its threshold size.

Section 3 of the paper contains an analysis of the cost-performance of LSM trees. This is based on the cost per unit of storage in each component (i.e. memory in C0, and disk in C1), and the cost per unit of I/O in each component. The Five-Minute Rule, which we examined earlier in the series (together with its updates at 10 and 20 years later) determines the inflection points where the dominant factors change.

This section also shows how to calculate the optimal threshold sizes for the various components in an LSM tree. The answer turns out to be to arrange things in a geometric progression whereby the ratio of the size of component(i) to the size of component(i+1) is a fixed value r for all adjacent components in the tree. The three variables ultimately affecting overall cost are therefore r, the size of component 0, and the number of components, k.

there are costs associated with increasing the number of components: a CPU cost to perform the additional rolling merges and a memory cost to buffer the nodes of those merges (which will actually swamp the memory cost of C0 in common cost regimes). In addition, indexed finds requiring immediate response will sometimes have to perform retrieval from all component trees. These considerations put a strong constraint on the appropriate number of components, and three components are probably the most that will be seen in practice.

http://blog.csdn.net/macyang/article/details/6677237

本文主要介绍了B+ tree和LSM tree，从seek和transfer的角度看Hbase为什么选择了LSM tree，而不是像大多数RDBMS那样使用B+ tree，在Hbase里面LSM tree这种结构其实就是由HLog + Memstore + StoreFile构成，HLog保存了顺序写入磁盘的日志，Memstore能够保存最近的数据，StoreFile负责存储Memstore flush的数据，另外背后有一些服务线程默默的做了很多事情，比如针对store files的compaction, 针对region的split, hlog file的roller等等。

Before we look into the architecture itself, however, we will first address a more fundamental difference between typical RDBMS storage structures and alternative ones. Specifically, we are going to have a quick look into B-trees, or rather B+ trees, as they are commonly used in relational storage engines, and Log-Structured Merge Trees, which (to some extent) form the basis for Bigtable's storage architecture, as discussed in the section called “Building Blocks”.

use the best strategy for the problem at hand
B+ trees have some specific features that allow for efficient insertion, lookup, and deletion of records that are identified by keys. They represent dynamic, multilevel indexes with lower and upper bounds as far as the number of keys in each segment (also called page) is concerned. Using these segments, they achieve a much higher fanout compared to binary trees, resulting in a much lower number of IO operations to find a specific key.

In addition, they also enable you to do range scans very efficiently, since the leaf nodes in the tree are linked and represent an in-order list of all keys, avoiding more costly tree traversals. That is one of the reasons why they are used for indexes in relational database systems.

In a B+ tree index, you get locality on a page-level (where page is synonymous to "block" in other systems): for example, the leaf pages look something like:

[link to previous page]

[link to next page]

key1 → rowid

key2 → rowid

key3 → rowid

In order to insert a new index entry, say key1.5, it will update the leaf page with a new key1.5 → rowid entry. That is not a problem until the page, which has a fixed size, exceeds its capacity. Then it has to split the page into two new ones, and update the parent in the tree to point to the two new half-full pages. See Figure 8.1, “An example B+ tree with one full page” for an example of a page that is full and would need to be split when adding another key.

The issue here is that the new pages aren't necessarily next to each other on disk. So now if you ask to query a range from key 1 to key 3, it's going to have to read two leaf pages which could be far apart from each other. That is also the reason why you will find an OPTIMIZE TABLE commands in most B+-tree based layouts - it basically rewrites the table in-order so that range queries become ranges on disk again.

Log-Structured Merge-Trees

LSM-trees, on the other hand, follow a different approach. Incoming data is stored in a log file first, completely sequentially. Once the log has the modification saved, it then updates an in-memory store that holds the most recent updates for fast lookup.

When the system has accrued enough updates and starts to fill up the in-memory store, it flushes the sorted list of key → record pairs to disk, creating a new store file. At this point, the updates to the log can be thrown away, as all modifications have been persisted.

The store files are arranged similar to B-trees, but are optimized for sequential disk access where all nodes are completely filled and stored as either single-page or multi-page blocks. Updating the store files is done in a rolling merge fashion, i.e., the system packs existing multi-page blocks together with the flushed in-memory data until the block reaches it full capacity.

Figure 8.2, “Multi-page blocks are iteratively merged across LSM trees” shows how a multi-page block is merged from the in-memory tree into the next on-disk one. Eventually the trees are kept merging into the larger ones.

As there are more flushes happening over time, creating many store files, a background process aggregates the files into larger ones so that disk seeks are limited to only a few store files. The on-disk tree can also be split into separate ones to spread updates across multiple store files. All of the stores are always sorted by the key, so no reordering is required ever to fit new keys in between existing ones.

Lookups are done in a merging fashion where the in-memory store is searched first, and then the on-disk store files next. That way all the stored data, no matter where it currently resides, forms a consistent view from a client's perspective.

Deletes are a special case of update wherein a delete marker is stored that is used during the lookup to skip "deleted" keys. When the pages are rewritten asynchronously, the delete markers and the key they mask are eventually dropped.

An additional feature of the background processing for housekeeping is the ability to support predicate deletions. These are triggered by setting a time-to-live (TTL) value that retires entries, for example, after 20 days. The merge processes will check the predicate and, if true, drop the record from the rewritten blocks.

The fundamental difference between the two, though, is how their architecture is making use of modern hardware, especially disk drives.

Comparing B+ trees and LSM-trees is about understanding where they have their relative strengths and weaknesses. B+ trees work well until there are too many modifications, because they force you to perform costly optimizations to retain that advantage for a limited amount of time. The more and faster you add data at random locations, the faster the pages become fragmented again. Eventually you may take in data at a higher rate than the optimization process takes to rewrite the existing files. The updates and deletes are done at disk seek rates, and force you to use one of the slowest metric a disk has to offer.

LSM-trees work at disk transfer rates and scale much better to handle vast amounts of data. They also guarantee a very consistent insert rate, as they transform random writes into sequential ones using the log file plus in-memory store. The reads are independent from the writes, so you also get no contention between these two operations.

The stored data is always in an optimized layout. So, you have a predictable and consistent bound on number of disk seeks to access a key, and reading any number of records following that key doesn't incur any extra seeks. In general, what could be emphasized about an LSM-tree based system is cost transparency: you know that if you have five storage files, access will take a maximum of five disk seeks. Whereas you have no way to determine the number of disk seeks a RDBMS query will take, even if it is indexed.

Seek vs. Sort and Merge in Numbers[85]

For our large scale scenarios computation is dominated by disk transfers. While CPU, RAM and disk size double every 18-24 months the seek time remains nearly constant at around 5% speed-up per year.

As discussed above there are two different database paradigms, one is Seek and the other Transfer. Seek is typically found in RDBMS and caused by the B-tree or B+ tree structures used to store the data. It operates at the disk seek rate, resulting in log(N) seeks per access.

Transfer on the other hand, as used by LSM-trees, sorts and merges files while operating at transfer rate and takes log(updates) operations. This results in the following comparison given these values:

10 MB/second transfer bandwidth

10 milliseconds disk seek time

100 bytes per entry (10 billion entries)

10 KB per page (1 billion pages)

When updating 1% of entries (100,000,000) it takes:

1,000 days with random B-tree updates

100 days with batched B-tree updates

1 day with sort and merge

We can safely conclude that at scale seek is simply inefficient compared to transfer.

http://liudanking.com/arch/lsm-tree-summary/

LSM Tree (Log-structured merge-tree) ：这个名称挺容易让人困惑的，因为你看任何一个介绍LSM Tree的文章很难直接将之与树对应起来。事实上，它只是一种分层的组织数据的结构，具体到实际实现上，就是一些按照逻辑分层的有序文件。

LSM Tree的树节点可以分为两种，保存在内存中的称之为MemTable, 保存在磁盘上的称之为SSTable

• 写操作直接作用于MemTable, 因此写入性能接近写内存。
• 每层SSTable文件到达一定条件后，进行合并操作，然后放置到更高层。合并操作在实现上一般是策略驱动、可插件化的。比如Cassandra的合并策略可以选择SizeTieredCompactionStrategy或LeveledCompactionStrategy.

• Level 0可以认为是MemTable的文件映射内存, 因此每个Level 0的SSTable之间的key range可能会有重叠。其他Level的SSTable key range不存在重叠。
• Level 0的写入是简单的创建-->顺序写流程，因此理论上，写磁盘的速度可以接近磁盘的理论速度。

• SSTable合并类似于简单的归并排序：根据key值确定要merge的文件，然后进行合并。因此，合并一个文件到更高层，可能会需要写多个文件。存在一定程度的写放大。是非常昂贵的I/O操作行为。Cassandra除了提供策略进行合并文件的选择，还提供了合并时I/O的限制，以期减少合并操作对上层业务的影响。

• 读操作优先判断key是否在MemTable, 如果不在的话，则把覆盖该key range的所有SSTable都查找一遍。简单，但是低效。因此，在工程实现上，一般会为SSTable加入索引。可以是一个key-offset索引（类似于kafka的index文件），也可以是布隆过滤器（Bloom Filter）。布隆过滤器有一个特性：如果bloom说一个key不存在，就一定不存在，而当bloom说一个key存在于这个文件，可能是不存在的。实现层面上，布隆过滤器就是key--比特位的映射。理想情况下，当然是一个key对应一个比特实现全映射，但是太消耗内存。因此，一般通过控制假阳性概率来节约内存，代价是牺牲了一定的读性能。对于我们的应用场景，我们将该概率从0.99降低到0.8，布隆过滤器的内存消耗从2GB+下降到了300MB，数据读取速度有所降低，但在感知层面可忽略。

• 基于LSM Tree存储引擎的数据适用于哪些场景？
  (key or key-range), 且key/key-range整体大致有序。

• LSM Tree本质上也是一种二分查找的思想，只是这种二分局限在key的大致有序这个假设上，并充分利用了磁盘顺序写的性能，但是普适性一般。B Tree对于写多读少的场景，大部分代价开销在Tree的维护上，但是具有更强的普适性。

看图轻松理解数据结构与算法系列(NoSQL存储-LSM树)